Notice
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- deep learning
- 코딩테스트
- FTP
- 프로토콜
- ICQA
- Machine learning
- IPV4
- 네트워크 관리사 2급
- Windows Server
- 딥러닝
- Protocol
- 알고리즘
- 실기
- network
- Python
- Django
- 자격증
- 네트워크 자격증
- Dynamic Programming
- 머신러닝
- 패스트캠퍼스
- dns
- 기본 정렬
- 밑바닥부터 시작하는 딥러닝
- 서브넷마스크
- 네트워크 관리사
- 파이썬
- 자료구조
- Algorithm
- 네트워크
Archives
- Today
- Total
쳉지로그
[밑바닥부터 시작하는 딥러닝] Chapter 5. 오차역전파법 본문
5.1 계산 그래프
5.1.1 계산 그래프로 풀다
- 계산 그래프: 계산 과정을 그래프로 나타낸 것 - 복수의 노드(node)와 에지(edge)로 표현
- 순전파(forward propagation): 그래프에서 계산을 왼쪽에서 오른쪽으로 진행하는 단계
- 억전파(backward propagation): 순전파의 반대 방향의 전파. 미분을 계산할 때 중요한 역할
5.1.2 국소적 계산
- 계산 그래프의 특징(이점) - '국소적 계산'을 전파함으로써 최종 결과를 얻음
- 국소적 계산은 전체에서 어떤 일이 벌어지든 상관없이 자신과 관계된 정보만으로 결과를 출력할 수 있다는 것
(참고) 국소적이란 '자신과 직접 관계된 작은 범위'라는 뜻
5.1.3 왜 계산 그래프로 푸는가?
- 전체가 아무리 복잡해도 각 노드에서는 단순한 계산에 집중하여 문제를 단순화할 수 있다.
- 계산 그래프는 중간 계산 결과를 모두 보관할 수 있다.
- 역전파를 통해 '미분'을 효율적으로 계산할 수 있다.

5.2 연쇄법칙
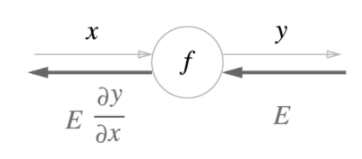
5.2.1 계산 그래프의 역전파
- 역전파의 계산 절차
- 신호 𝑬 에 노드의 국소적 미분(𝝏𝒚/𝝏𝒙)을 곱한 후, 다음 노드로 전달
5.2.2 연쇄법칙이란?
- 합성 함수: 여러 함수로 구성된 함수
- 연쇄법칙(Chain Rule) 원리:
- 합성 함수의 미분은 합성 함수를 구성하는 각 함수의 미분의 곱으로 나타낼 수 있다.
'머신러닝 > 밑바닥부터 시작하는 딥러닝' 카테고리의 다른 글
| [밑바닥부터 시작하는 딥러닝] Chapter 7. 합성곱 신경망(CNN) (1) (0) | 2021.05.09 |
|---|---|
| [밑바닥부터 시작하는 딥러닝] Chapter 4. 신경망 학습(2) (0) | 2021.04.21 |
| [밑바닥부터 시작하는 딥러닝] Chapter 4. 신경망 학습(1) (0) | 2021.04.21 |
| [밑바닥부터 시작하는 딥러닝] Chapter 3. 신경망 (0) | 2021.04.14 |
| [밑바닥부터 시작하는 딥러닝] Chapter 2. 퍼셉트론 (0) | 2021.04.14 |
Comments




