| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- 자료구조
- Windows Server
- Django
- Dynamic Programming
- 알고리즘
- 네트워크 관리사
- 서브넷마스크
- 자격증
- 밑바닥부터 시작하는 딥러닝
- 코딩테스트
- 네트워크 자격증
- ICQA
- 프로토콜
- 기본 정렬
- dns
- 네트워크 관리사 2급
- Algorithm
- deep learning
- 실기
- IPV4
- FTP
- 딥러닝
- Python
- 네트워크
- Machine learning
- network
- 패스트캠퍼스
- Protocol
- 파이썬
- 머신러닝
- Today
- Total
쳉지로그
[밑바닥부터 시작하는 딥러닝] Chapter 3. 신경망 본문
3.1 퍼셉트론에서 신경망으로
3.1.1 신경망의 예
신경망 : 입력층(input layer), 은닉층(hidden layer), 출력층(output layer)으로 구성
- 입력층, 출력층의 뉴런은 눈에 보이는 층
- 은닉층의 뉴런은 눈에 보이지 않는 층
- 층 번호는 0부터 시작

3.1.2 퍼셉트론 복습
퍼셉트론 : 다수의 신호를 입력으로 받아 하나의 신호를 출력하는 알고리즘

- 𝑏 : 편향을 나타내는 매개변수 (뉴런이 얼마나 쉽게 활성화되느냐를 제어)
- 𝑤1, 𝑤2 : 가중치를 나타내는 매개변수 (각 신호의 영향력을 제어)
편향을 명시한 퍼셉트론: 가중치가 𝑏이고, 입력이 1인 뉴런이 추가

3.1.3 활성화 함수의 등장
활성화 함수(activation function) : 입력 신호의 총합을 출력 신호로 변환하는 함수 (위의 h(x))

3.2 활성화 함수
- 위의 h(x)와 같은 함수를 **계단 함수(step function)**이라 함
- 즉, 퍼셉트론에서는 활성화 함수로 계단 함수를 이용한다.
3.2.1 시그모이드 함수
시그모이드 함수(sigmoid function) : 신경망에서 자주 이용하는 활성화 함수

- 신경망에서는 활성화 함수로 시그모이드 함수를 이용하여 신호를 변환하고, 그 변환된 신호를 다음 뉴런에 전달한다.
3.2.2 계단 함수 구현하기

3.2.3 계단 함수의 그래프


3.2.4 시그모이드 함수 구현하기


3.2.5 시그모이드 함수와 계단 함수 비교
공통점
- 입력이 작을 때의 출력은 0에 가깝고(혹은 0이고), 입력이 커지면 출력이 1에 가까워지는(혹은 1이 되는) 구조
- 비선형 함수
차이점
- 시그모이드 함수
- 부드러운 곡선, 입력에 따라 출력이 연속적으로 변화
- 실수(0.731..., 0.880... 등)를 반환
- 계단 함수
- 0을 경계로 출력이 갑자기 바뀜
- 0과 1중 하나의 값만 반환
3.2.6 비선형 함수
- 계단 함수와 시그모이드 함수의 중요한 공통점
- 시그모이드 함수는 곡선, 계단 함수는 계단처럼 구부러진 직선으로 나타나며, 동시에 비선형 함수로 분류됨
(참고)
선형 함수 : 출력이 입력의 상수배만큼 변하는 함수 (f(x) = ax + b)
비선형 함수: 선형이 아닌 함수
- 신경망에서 활성화 함수로 비선형 함수를 사용하는 이유?⇒ 그렇기 때문에 층을 쌓는 혜택을 얻기 위해서는 반드시 비선형 함수를 사용해야 함
- ⇒ 선형 함수는 층을 아무리 깊게 해도 은닉층이 없는 네트워크로도 똑같은 기능을 할 수 있음
3.2.7 ReLU 함수
- 시그모이드 함수는 신경망 분야에서 오래전부터 이용해왔으나, 최근에는 ReLU 함수를 주로 이용
ReLU(Rectified Linear Unit) 함수 : 입력이 0을 넘으면 그 입력을 그대로 출력하고, 0 이하이면 0을 출력하는 함수

3.3 다차원 배열의 계산
3.3.1 다차원 배열

3.3.2 행렬의 곱

3.3.3 신경망에서의 행렬 곱

3.4 3층 신경망 구현하기
- 3층 신경망: 입력층(0층)은 2개 첫 번째 은닉층(1층)은 3개, 두 번째 은닉층(2층)은 2개, 출력층(3층)은 2개의 뉴런으로 구성된다.

3.4.1 표기법 설명

3.4.2 각 층의 신호 전달 구현하기
1. 편향을 뜻하는 뉴런 1 추가 & 다차원 배열을 사용해서 식 구현


2. 활성화 함수(시그모이드 함수)의 처리


3. 1층에서 2층으로 가는 과정 살펴보기
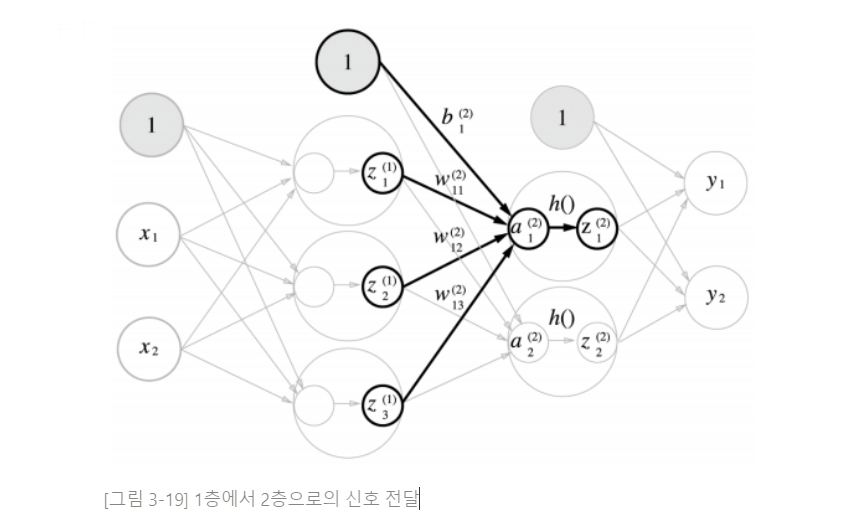

4. 2층에서 출력층으로의 신호 전달 (활성화 함수 = 항등 함수)


- 항등 함수 : 입력을 그대로 출력하는 함수 identity_function()
- 출력층의 활성화 함수를 **σ()**로 표시하여 은닉층의 활성화 함수 h()와는 다름을 명시
3.4.3 구현 정리

3.5 출력층 설계하기
- 신경망은 분류와 회귀 모두에 이용할 수 있음
- 일반적으로 **회귀(regression)에는 항등 함수를, 분류(classification)**에는 소프트맥스 함수를 사용
(참고)
회귀(regression) : 입력 데이터에서 (연속적인) 수치를 예측하는 문제
분류(classification) : 데이터가 어느 클래스에 속하느냐는 문제
3.5.1 항등 함수와 소프트맥스 함수 구현하기
- 항등 함수(identity function)
- -출력층에서 항등 함수를 사용하면 입력 신호가 그대로 출력 신호가 됨

- 소프트맥스 함수(softmax function)
- exp(x) : 𝑒^𝑥 을 뜻하는 지수 함수(exponential function) (e는 자연상수)
- 𝑛 : 출력층의 뉴런 수
- 𝑦𝑘 : k번째 출력
- 𝑎𝑘 : 입력 신호
- 소프트맥스의 출력은 모든 입력 신호로부터 화살표를 받음



3.5.2 소프트맥스 함수 구현 시 주의점
- 컴퓨터로 계산할 때 오버플로(overflow) 문제 발생
(참고)
오버플로(overflow) : 표현할 수 있는 수의 범위가 한정되어 너무 큰 값은 표현할 수 없다는 문제
개선한 소프트맥스 함수 수식



3.5.3 소프트맥스 함수의 특징
- 소프트맥스 함수의 출력은 0에서 1.0 사이의 실수
- 소프트맥스 함수 출력의 총합은 1 ⇒ 소프트맥스 함수의 출력을 '확률'로 해석할 수 있음
- 소프트맥스 함수를 적용해도 각 원소의 대소 관계는 변하지 않음
3.5.4 출력층의 뉴런 수 정하기
- 출력층의 뉴런 수는 풀려는 문제에 맞게 적절히 정해야 함
- 분류 ⇒ 분류하고 싶은 클래스 수로 설정하는 것이 일반적
- 뉴런의 회색 농도가 해당 뉴런의 출력 값의 크기를 의미 (짙을 수록 큰 값)

3.6 손글씨 숫자 인식
신경망의 문제 해결 두 단계
- 학습 단계 : 훈련 데이터(학습 데이터)를 사용해 가중치 매개변수를 학습.
- 추론 단계 : 앞서 학습한 매개변수를 사용하여 입력 데이터를 분류
신경망의 순전파(forward propagation) : 추론 과정
3.6.1 MNIST 데이터셋
MNIST : 손글씨 숫자 이미지 집합
- 0부터 9까지의 숫자 이미지로 구성
- 훈련 이미지 : 60,000장, 시험 이미지 : 10,000장


load_mnist()
- 읽은 MNIST 데이터를 "(훈련 이미지, 훈련 레이블), (시험 이미지, 시험 레이블)" 형식으로 반환
- 세 가지 설정 (세 인수 모두 bool 값)
- normalize :
- (True) 입력 이미지의 픽셀 값을 0.0~1.0사이의 값으로 정규화
- (False) 0~255 사이의 값 유지
- flatten : 입력 이미지를 1차원 배열로 만들지 결정
- (True) 784개의 원소로 이루어진 1차원 배열로 저장
- (False) 입력 이미지를 1x28x28 3차원 배열로 저장
- one_hot_label : 레이블을 one-hot encoding 형태로 저장할지 결정
- (True) [0, 0, 1, 0, 0, 0, 0, 0, 0] 처럼 정답을 뜻하는 원소만 1이고 나머지는 0
- (False) ‘7’, ‘2’와 같이 숫자 형태의 레이블 저장
3.6.2 신경망의 추론 처리
신경망 구현
- 입력층 뉴런 784개(이미지의 크기가 28x28), 출력층 뉴런 10개(0~9까지의 숫자)
- 은닉층 2개 : 첫 번째 은닉층 뉴런 50개, 두 번째 은닉층 뉴런 100개

(참고)
정규화(normalization) : 데이터를 특정 범위로 변환하는 처리
전처리(pre-processing) : 신경망의 입력 데이터에 특정 변환을 가하는 것
3.6.3 배치 처리
배치(batch) : 하나로 묶은 입력 데이터

'머신러닝 > 밑바닥부터 시작하는 딥러닝' 카테고리의 다른 글
| [밑바닥부터 시작하는 딥러닝] Chapter 5. 오차역전파법 (0) | 2021.04.28 |
|---|---|
| [밑바닥부터 시작하는 딥러닝] Chapter 4. 신경망 학습(2) (0) | 2021.04.21 |
| [밑바닥부터 시작하는 딥러닝] Chapter 4. 신경망 학습(1) (0) | 2021.04.21 |
| [밑바닥부터 시작하는 딥러닝] Chapter 2. 퍼셉트론 (0) | 2021.04.14 |
| [밑바닥부터 시작하는 딥러닝] Chapter 1. 헬로 파이썬 (0) | 2021.04.14 |




